PDP-11/45: Diagnostics XIII - FP11 FPU, cont.
Thu 24 November 2016 by Fritz MuellerHave been looking into the FP11 MOD problem in spare moments of the past few weeks, but haven't written up an account of the progress, so this will be a bit of a catch-up article.
Having now studied the design of this thing in more depth, there are a few things I find interesting:
-
The inner loops of the multiplication, division, and floating-point normalization algorithms on the FP11 are not implemented in microcode, but rather as "hardware subroutines". Microcode does all the setup of the various internal registers and counters, then pauses while the hardware runs the inner loop, then picks up again to mediate rounding, masking, exceptions, etc. afterward.
-
The multiplication implementation uses an interesting algorithm called "skipping over ones and zeros", described in section 5.3.1 of the FP11 maintenance manual. This reduces the number of time-consuming additions needed on average. It works along the lines of a familiar mental shortcut: suppose you had to multiply some number X by 999. Rather than multiply X by 9 three times and shift and add them all up, you would probably just take X * 1,000 and subtract off X * 1. The key observation is that you can do this for any contiguous string of 9s in the multiplier: subtract the multiplicand from the partial product at the place value where the string begins, then add the multiplicand at one past place value where the string ends. The FP11 implements the binary equivalent of this with a small state machine (comprised of flip-flops MR1, MR0, and STRG1) which identifies strings of contiguous 1s and invokes ALU subtractions and additions on the boundaries as the multiplier is shifted through.
-
Debugging techniques: a KM11 in single-clock-transition mode may be used to step within the hardware subroutines, as they are driven off the main FP11 clock. It can be a lot of switch presses to step through an entire multiply (120 or so clock transitions at least for a double-precision multiply, and typically more because each necessary intermediate add/subtract adds eight clock transitions!) and this gets to be pretty tedious and error-prone. A logic analyzer is very useful here to capture a visualization of an entire multiplication at one go, and enable counting off clock transitions needed to get to something you'd like to take a closer look at with a logic probe. Alternatively, if your FP11 is working well enough to run maintenance instructions, there are software techniques that can prematurely terminate the hardware subroutines and also give some useful visibility into the intermediate states.
I opted to try out the software techniques to see if I could get more information on the (mis)behavior in my FP11 order to focus my hardware troubleshooting. The following program came in handy. This is based off some example code in the FP11 maintenance manual, though I elaborated it slightly with a binary printout routine:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 | 000000 AC0=%0
000001 AC1=%1
000002 AC2=%2
177560 SERIAL=177560
170006 MRS=170006
000000 .ASECT
001000 .=1000
001000 170127 040220 START: LDFPS #40220 ;DISABLE INTS, SET DBL AND MAINT MODE
001004 172667 000316 LDD MLYR,AC2 ;LOAD MULTIPLIER IN AC2
001010 012703 000230 MOV #230,R3 ;R3 GETS OCTAL 230 (FRAC MUL MICROSTATE)
001014 170003 LDUB ;LOAD R3 TO MBR
001016 012702 177564 MOV #SERIAL+4,R2 ;SERIAL XMIT BASE TO R2
001022 012762 000015 000002 MOV #15,2(R2) ;OUTPUT '\R'
001030 105712 TSTB (R2) ;CHECK XMIT CLEAR
001032 100376 BPL .-2 ;LOOP UNTIL SO
001034 012762 000012 000002 MOV #12,2(R2) ;OUTPUT '\N'
001042 105712 TSTB (R2) ;CHECK XMIT CLEAR
001044 100376 BPL .-2 ;LOOP UNTIL SO
001046 005004 CLR R4 ;R4 HOLDS SC VALUE
001050 005204 NXTMUL: INC R4 ;INCREMENT SC
001052 170004 LDSC ;LOAD 1S COMPLEMENT OF R4 INTO SC
001054 012705 001356 LSTMUL: MOV #QR+10,R5 ;SET R5 PAST END OF STORAGE TABLE
001060 172567 000232 LDD MCND,AC1 ;LOAD MULTIPLICAND INTO AC1
001064 171102 MULD AC2,AC1 ;DO PARTIAL MULTIPLY
001066 170007 STQ0 ;TRANSFER QR TO AC0
001070 174045 STD AC0,-(R5) ;STORE QR IN TABLE
001072 042715 177600 BIC #177600,(R5) ;CLEAR OFF SIGN AND EXPONENT
001076 170005 STA0 ;TRANSFER AR TO AC0
001100 174045 STD AC0,-(R5) ;STORE AR IN TABLE
001102 042715 177600 BIC #177600,(R5) ;CLEAR OFF SIGN AND EXPONENT
001106 170006 MRS ;SHIFT AR AND QR RIGHT ONE PLACE
001110 170006 MRS ;SHIFT AR AND QR RIGHT ONE PLACE
001112 170007 STQ0 ;TRANSFER QR TO AC0
001114 174067 000236 STD AC0,TEMP ;STORE QR IN TEMP
001120 016703 000232 MOV TEMP,R3 ;FETCH MSW OF QR TO R3
001124 042703 177600 BIC #177600,R3 ;CLEAR OFF SIGN AND EXPONENT
001130 006303 ASL R3 ;SHIFT MSBS OF QR ONE PLACE LEFT
001132 006303 ASL R3 ;SHIFT MSBS OF QR ONE PLACE LEFT
001134 050365 000010 BIS R3,10(R5) ;SET QR59 AND QR58 IN TABLE
001140 170005 STA0 ;TRANSFER AR TO AC0
001142 174067 000210 STD AC0,TEMP ;STORE AR IN TEMP
001146 016703 000204 MOV TEMP,R3 ;FETCH MSW OF AR TO R3
001152 042703 177600 BIC #177600,R3 ;CLEAR OFF SIGN AND EXPONENT
001156 006303 ASL R3 ;SHIFT MSBS OF AR ONE PLACE LEFT
001160 006303 ASL R3 ;SHIFT MSBS OF AR ONE PLACE LEFT
001162 050315 BIS R3,(R5) ;SET AR59 AND AR58 IN TABLE
001164 012705 001336 MOV #AR,R5 ;GET ADDRESS OF FIRST QUAD FOR PRINTING
001170 012700 000010 MOV #10,R0 ;R0 COUNTS 8 WORDS IN TWO QUADS
001174 012503 LWORD: MOV (R5)+,R3 ;FETCH NEXT WORD OF QUAD
001176 012701 000020 MOV #20,R1 ;R1 COUNTS 16 BITS IN WORD
001202 006103 LBIT: ROL R3 ;ROTATE, HIGH BIT GOES TO CARRY
001204 103405 BCS LBIT1 ;SKIP AHEAD IF CARRY SET
001206 012762 000056 000002 MOV #56,2(R2) ;OTHERWISE OUTPUT '.'
001214 000167 000006 JMP LBIT2 ;AND SKIP AHEAD
001220 012762 000061 000002 LBIT1: MOV #61,2(R2) ;OUTPUT '1'
001226 105712 LBIT2: TSTB (R2) ;CHECK XMIT CLEAR
001230 100376 BPL .-2 ;LOOP UNTIL SO
001232 077115 SOB R1,LBIT ;LOOP OVER BITS IN WORD
001234 012762 000040 000002 MOV #40,2(R2) ;OUTPUT ' ' TO SEPARATE WORDS
001242 105712 TSTB (R2) ;CHECK XMIT CLEAR
001244 100376 BPL .-2 ;LOOP UNTIL SO
001246 077026 SOB R0,LWORD ;LOOP OVER WORDS IN QUAD
001250 012762 000015 000002 MOV #15,2(R2) ;OUTPUT '\R'
001256 105712 TSTB (R2) ;CHECK XMIT CLEAR
001260 100376 BPL .-2 ;LOOP UNTIL SO
001262 012762 000012 000002 MOV #12,2(R2) ;OUTPUT '\N'
001270 105712 TSTB (R2) ;CHECK XMIT CLEAR
001272 100376 BPL .-2 ;LOOP UNTIL SO
001274 020427 000071 CMP R4,#71 ;CHECK PASSES AGAINST 57
001300 100663 BMI NXTMUL ;LESS: DO NEXT PASS
001302 001402 BEQ LSTPAS ;EQUAL: DO LAST PASS
001304 000167 171470 JMP 173000 ;GREATER: RETURN TO M9301 MONITOR
001310 005204 LSTPAS: INC R4 ;INDICATE 58TH PASS
001312 000167 177536 JMP LSTMUL ;DO LAST PASS WITHOUT LOADING SC
001316 040200 000000 000000 MCND: .WORD 040200, 000000, 000000, 000000
001324 000000
001326 040300 000300 000300 MLYR: .WORD 040300, 000300, 000300, 000300
001334 000300
001336 000000 000000 000000 AR: .FLT4 0
001344 000000
001346 000000 000000 000000 QR: .FLT4 0
001354 000000
001356 000000 000000 000000 TEMP: .FLT4 0
001364 000000
001000 .END START
|
The idea here is to use the LDUB (load micro-break) and LDSC (load step-counter) maintenance instructions to cause a multiplication to halt partway through. STA0 and STQ0 (store AR, store QR) instructions, in conjunction with the MRS (maintenance right shift) instruction, allow retrieval of the internal fraction registers which are then printed out to the serial console. This is done repetitively, stopping each time one step further on, so the progression of the internal states of AR and QR over the course of the entire multiply may be observed.
A quick aside here on tooling: since I don't currently have any storage or an OS running on my PDP-11, I load and execute diagnostics with PDP11GUI to an M9301 boot monitor over a serial connection. This requires program binaries in LDA (absolute loader) format. For non-trivial MACRO-11 programs I have found it most convenient to use the actual vintage toolchain under RT-11 in the simh simulator, because the assembler and linker provided with PDP11GUI have some limitations. I copy files in and out via the simulated paper tape reader/punch. This is also how I produce the MACRO-11 listings seen on this blog.
Okay, back to the program above, running this on my machine very clearly illustrates the malfunction. Here's what the output looks like:
................ ................ ................ ................ .........11..... .........11..... .........11..... .........11..... ................ ................ ................ ................ ..........11.... ..........11.... ..........11.... ..........11.... ................ ................ ................ ................ ...........11... ...........11... ...........11... ...........11... ................ ................ ................ ................ ............11.. ............11.. ............11.. ............11.. ................ ................ ................ ................ .............11. .............11. .............11. .............11. ................ ................ ................ ................ ..............11 ..............11 ..............11 ..............11 ................ ................ ................ ................ ...............1 1..............1 1..............1 1..............1 .......11.111111 1111111111111111 1111111111111111 1111111111111111 ................ 11.............. 11.............. 11.............. .......111.11111 1111111111111111 1111111111111111 1111111111111111 ................ .11............. .11............. .11............. ..........1.1111 1111111111111111 1111111111111111 1111111111111111 ................ ..11............ ..11............ ..11............ ...........1.111 1111111111111111 1111111111111111 1111111111111111 ................ ...11........... ...11........... ...11........... ............1.11 1111111111111111 1111111111111111 1111111111111111 ................ ....11.......... ....11.......... ....11.......... .............1.1 1111111111111111 1111111111111111 1111111111111111 ................ .....11......... .....11......... .....11......... ..............1. 1111111111111111 1111111111111111 1111111111111111 ................ ......11........ ......11........ ......11........ ...............1 .111111111111111 1111111111111111 1111111111111111 ................ .......11....... .......11....... .......11....... ................ 1.11111111111111 1111111111111111 1111111111111111 ................ ........11...... ........11...... ........11...... ................ .1.1111111111111 1111111111111111 1111111111111111 ................ .........11..... .........11..... .........11..... ................ ..1.111111111111 1111111111111111 1111111111111111 ................ ..........11.... ..........11.... ..........11.... ................ ...1.11111111111 1111111111111111 1111111111111111 ................ ...........11... ...........11... ...........11... ................ ....1.1111111111 1111111111111111 1111111111111111 ................ ............11.. ............11.. ............11.. ................ .....1.111111111 1111111111111111 1111111111111111 ................ .............11. .............11. .............11. ................ ......1.11111111 1111111111111111 1111111111111111 ................ ..............11 ..............11 ..............11 ................ .......1.1111111 1111111111111111 1111111111111111 ................ ...............1 1..............1 1..............1 .......111...... ........1.111111 1111111111111111 1111111111111111 ................ ................ 11.............. 11.............. .......1111..... .........1.11111 1111111111111111 1111111111111111 ................ ................ .11............. .11............. ..........11.... ..........1.1111 1111111111111111 1111111111111111 ................ ................ ..11............ ..11............ ...........11... ...........1.111 1111111111111111 1111111111111111 ................ ................ ...11........... ...11........... ............11.. ............1.11 1111111111111111 1111111111111111 ................ ................ ....11.......... ....11.......... .............11. .............1.1 1111111111111111 1111111111111111 ................ ................ .....11......... .....11......... ..............11 ..............1. 1111111111111111 1111111111111111 ................ ................ ......11........ ......11........ ...............1 1..............1 .111111111111111 1111111111111111 ................ ................ .......11....... .......11....... ................ 11.............. 1.11111111111111 1111111111111111 ................ ................ ........11...... ........11...... ................ .11............. .1.1111111111111 1111111111111111 ................ ................ .........11..... .........11..... ................ ..11............ ..1.111111111111 1111111111111111 ................ ................ ..........11.... ..........11.... ................ ...11........... ...1.11111111111 1111111111111111 ................ ................ ...........11... ...........11... ................ ....11.......... ....1.1111111111 1111111111111111 ................ ................ ............11.. ............11.. ................ .....11......... .....1.111111111 1111111111111111 ................ ................ .............11. .............11. ................ ......11........ ......1.11111111 1111111111111111 ................ ................ ..............11 ..............11 ................ .......11....... .......1.1111111 1111111111111111 ................ ................ ...............1 1..............1 .......111...... ........11...... ........1.111111 1111111111111111 ................ ................ ................ 11.............. .......1111..... .........11..... .........1.11111 1111111111111111 ................ ................ ................ .11............. ..........11.... ..........11.... ..........1.1111 1111111111111111 ................ ................ ................ ..11............ ...........11... ...........11... ...........1.111 1111111111111111 ................ ................ ................ ...11........... ............11.. ............11.. ............1.11 1111111111111111 ................ ................ ................ ....11.......... .............11. .............11. .............1.1 1111111111111111 ................ ................ ................ .....11......... ..............11 ..............11 ..............1. 1111111111111111 ................ ................ ................ ......11........ ...............1 1..............1 1..............1 .111111111111111 ................ ................ ................ .......11....... ................ 11.............. 11.............. 1.11111111111111 ................ ................ ................ ........11...... ................ .11............. .11............. .1.1111111111111 ................ ................ ................ .........11..... ................ ..11............ ..11............ ..1.111111111111 ................ ................ ................ ..........11.... ................ ...11........... ...11........... ...1.11111111111 ................ ................ ................ ...........11... ................ ....11.......... ....11.......... ....1.1111111111 ................ ................ ................ ............11.. ................ .....11......... .....11......... .....1.111111111 ................ ................ ................ .............11. ................ ......11........ ......11........ ......1.11111111 ................ ................ ................ ..............11 ................ .......11....... .......11....... .......1.1111111 ................ ................ ................ ...............1 .......111...... ........11...... ........11...... ........1.111111 ................ ................ ................ ................ .......1111..... .........11..... .........11..... .........1.11111 ................ ................ ................ ................ .........11..... .........11..... .........11..... .........1.11111 ................ ................ ................ ................
The left half of the output above shows the contents of AR throughout the progress of the multiply, and the right half shows the contents of QR. The most significant 57 bits of each are shown, right justified in a 64-bit field.
In the FP11, as the multiplication proceeds, the multiplicand is held constant, while the multiplier (in QR) and partial product (in AR) are successively right shifted. The bits of the multiplier involved in the skip-over-ones-and-zeros sate macheine are QR3 and QR2. QR3 is the rightmost bit shown above. QR2, to its right, is not retrievable by software and thus not shown.
Since the multiplicand in the sample code is 1.0, the result left in AR (bottom row of left half) should be identical with the initial value of the multiplier in QR (top row of right half), but clearly something is amiss with the least significant bits of the result. We can also see that things go awry as the first string off consecutive 1s starts through the state machine (adjusting the values in the test program shows that this is always the case). So this looks like an issue with the state machine or the FALU control signals that derive from it. Taking a look with the logic analyzer shows this:
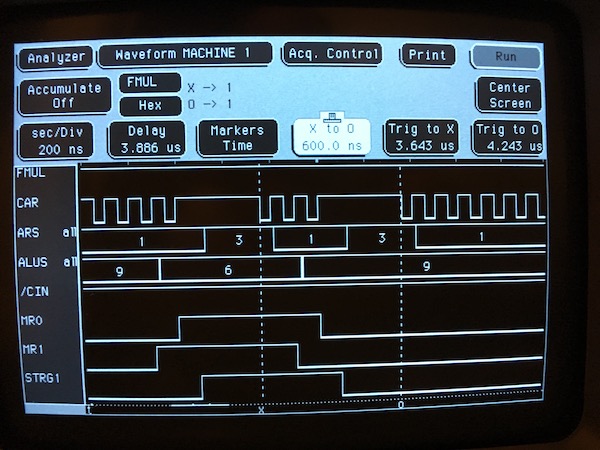
This is a portion of the multiply dealing with the a string of two consecutive 1s on the multiplier. The clocking and state machine state bits look correct (note that AR clocks falling edges). A four-cycle pause is inserted in the AR clock whenever the state-machine dictates either an add or a subtract is to occur, in order to allow for propagation time through the ALUs. The AR and ALU function selects also look correct: AR 1 for shift, 3 for load, and ALU 6 for subtract, 9 for add. Marker X here should be clocking in a subtraction at the start of the string, followed by two shifts, then an add at marker O at the end of the string.
But the ALU CIN control signal looks incorrect -- it is held high throughout the multiply, but should be driven low for the subtraction at marker X. This means the ALU function actually being selected is A-B-1 instead of A-B, which would produce the results seen above (the first subtract borrows an extra 1 all the way across the partial product, then subsequent subtracts borrow from the resulting 1s on the right). So it looks like the logic that generates CIN needs a look:
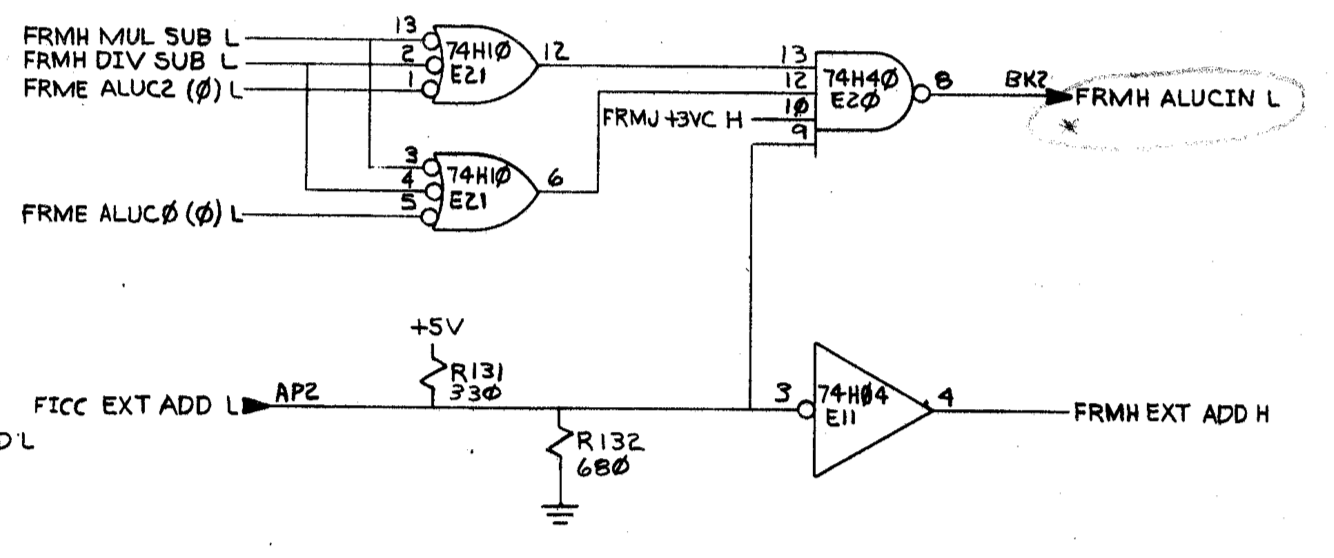
Stepping through the multiply with the KM11 in single-clock-transition mode, arriving at the first subtract, FRMH MUL SUB L is asserted low to pin 3 of E21, but pin 6 does not go high. Looks like a failed gate; pulled the part, put in a socket, and put a replacement 74H10 on order. All for now!